
1- Abstract.
2- Introduction.
3- Equation.
4- Length Of Lunar Orbit.
5- Ocean Friction.
6- Inertial Earth-Moon System.
7- Compare.
You cannot talk about the speed of light without defining your frame of reference. The measured speed of light in "local inertial frames" is 299792.458 km/sec. So if you want to make a comparison with "299792.458 km/sec" then you have to make it in a "local inertial frame".
Special Relativity requires the frame of reference to be inertial (travel in a straight line). Since Earth (our local frame of reference) is orbiting the sun then it is not traveling in a straight line, hence it is non-inertial. So when we compare the nominal speed of light with 12000 Lunar Orbits / Earth Day inside the gravitational field of the sun (non-inertial frame) we get 11% difference; however when the geocentric frame is inertial we get zero% difference.
As long as Earth is not traveling in a straight line then any geocentric frame is non-inertial, hence NASA's measurement of the lunar orbit is made in a non-inertial frame. So we have to calculate the lunar orbit in an inertial frame starting from the measured one in this non-inertial frame. We need to calculate 12000 Lunar Orbits / Earth Day when the geocentric frame travels in a straight line; on the other hand we already know that outside sun's gravity it would travel in a straight line. But from the equivalence principle we know that these two experiments are equivalent, that is, whenever Earth is inertial you will get the same results as if Earth is outside sun's gravity. We chose to calculate the lunar orbit outside sun's gravity because it is easier to calculate however these two experiments are absolutely identical.
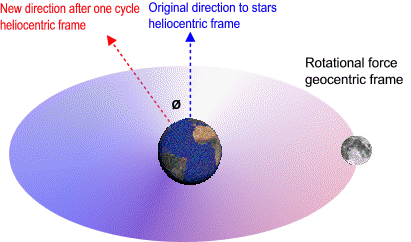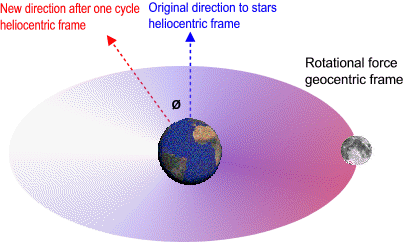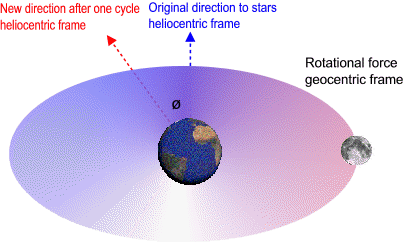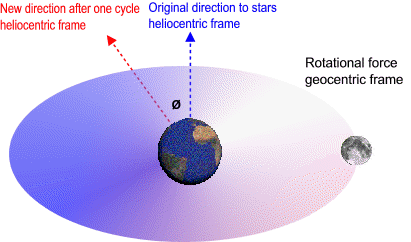
In a local frame non-rotating with respect to sun the moon speeds up when it heads towards the sun and then slows down by the same amount when it heads away from the sun. However in a local frame non-rotating with respect to stars the sectors where the moon speeds up and slows down are actually moving forward inside the orbit by the same angle Earth orbits the sun. In this frame there is a rotational force around Earth. This means that the lunar orbit is influenced by a torque-like force around Earth (twist, assist). As the distance to the sun increases to infinity the lunar orbit loses this twist. When we remove the energy gained from this twist we can calculate the total energy and hence the length of the lunar orbit outside gravitational fields. When the Earth-moon system exits the solar system the geocentric frame travels in a straight line (becomes inertial) and 12000 Lunar Orbits / Earth Day becomes equivalent to the speed of light. The difference in this local inertial frame is 0.01%.
Have you noticed that when you spin on your toes your clothes fling outwards? And that when your spin slows down your clothes settle back inwards? This is what also happens when the Earth-moon system gains or loses rotational kinetic energy, the distance to the moon changes (hence the length of the lunar orbit changes).
Do you know why the same half of the moon always faces Earth? The moon has been facing Earth like this for more than 4 billion years. Just like Earth rotates on its axis once every day with respect to stars, the moon also rotates on its axis with respect to stars. Since the moon keeps facing Earth this means that the moon needs to orbit Earth once in order for the moon to spin once on its axis with respect to stars. When the moon first formed it was very close to Earth and it orbited Earth once every few hours, today this period is 27 days, and as the moon continues to recede this period will continue to increase; the greater the distance from Earth the greater this period becomes. When this period becomes 50 days, for example, this also means that it will take the moon 50 days to spin 360 degrees on its axis with respect to stars. So as the moon recedes from Earth its spin with respect to stars slows down, that is, it loses rotational kinetic energy (this is different from moon's kinetic energy due to moon's motion around Earth). If the distance to Earth increases to infinity, the moon would stop spinning with respect to stars and hence its rotational kinetic energy decreases to zero. This proves that the moon's rotational kinetic energy is a function of the distance from Earth. Similarly the total energy of the Earth-moon system is a function of the distance from the sun, that is, as the distance to the sun changes the total energy of the Earth-moon system changes, hence the length of the lunar orbit changes.
From Special Relativity we know that in a heliocentric frame non-rotating with respect to stars light travels in a straight line, hence this is an inertial frame. However in this frame Earth DOES NOT travel in a straight line, hence the geocentric frame is non-inertial:

In a geocentric frame non-rotating with respect to sun the moon speeds up when it heads towards the sun and then slows down by the same amount when it heads away from the sun. However in a geocentric frame non-rotating with respect to stars the sectors where the moon speeds up and slows down are actually moving forward inside the orbit by the same angle Earth orbits the sun. In this frame there is a rotational force around Earth. This means that the lunar orbit is influenced by a torque-like force around Earth (twist, assist). As the distance to the sun increases to infinity θ decreases to zero and lunar orbit loses this twist. When we remove the energy gained from this twist we can calculate the total energy and hence the length of the lunar orbit outside gravitational fields.
C t' = 12000 L'
Where:
C is the speed of light.
t' is Earth Day outside gravitational fields i.e. time for one rotation of Earth about its axis with respect to stars.
L' is the length of the lunar orbit outside gravitational fields (no external forces, no acceleration, no deceleration).
This table below shows the lunar month and Earth day in both sidereal system (with respect to stars) and synodic (with respect to sun):

Every new moon (29.5 days) the moon will not return to the same point in the orbit (it will be at a different point). The moon returns to the same point in the orbit after only 27.3 days. When the moon returns to the same point with respect to stars the Earth-moon system would have moved 26.9 degrees around the sun (not 29.1 degrees):

Any astronomical measurement depends on the frame of reference. Your frame of reference is your clock and coordinate system (your ruler/axis and its orientation/rotation). When measuring 12000 Lunar Orbits/Earth Day in km/sec you could define million different frames and get million different results. However historically two geocentric frames were popular: the synodic and the sidereal systems. Both qualify as local frames however they differ by their rotation. The sidereal system is a local frame non-rotating with respect to stars, while the synodic system is a local frame non-rotating with respect to sun. Historically people used the lunar calendar and their month was 29.5 Earth days which means they used the synodic system. The synodic system is a local frame non-rotating with respect to sun; however this frame is rotating with respect to stars.
The animation below shows you the difference; the left side has two superimposed frames, one non-rotating with respect to sun (x,y) plus another one non-rotating with respect to stars (X',Y'). The right side has just one frame non-rotating with respect to sun (x,y).
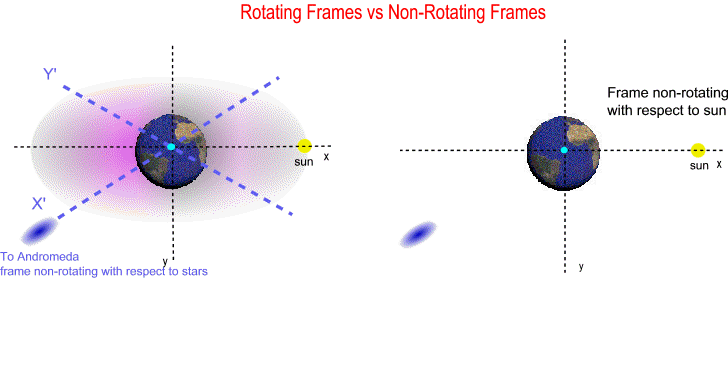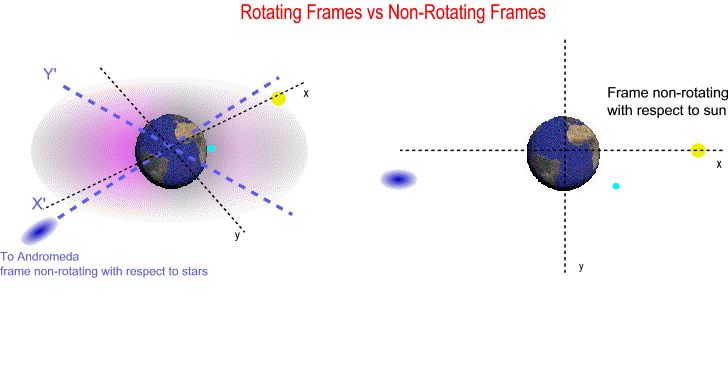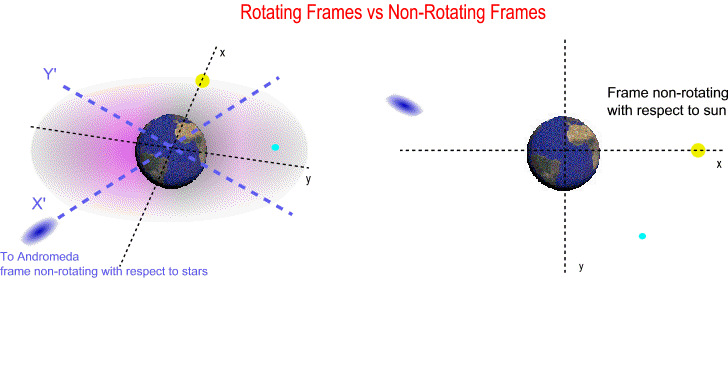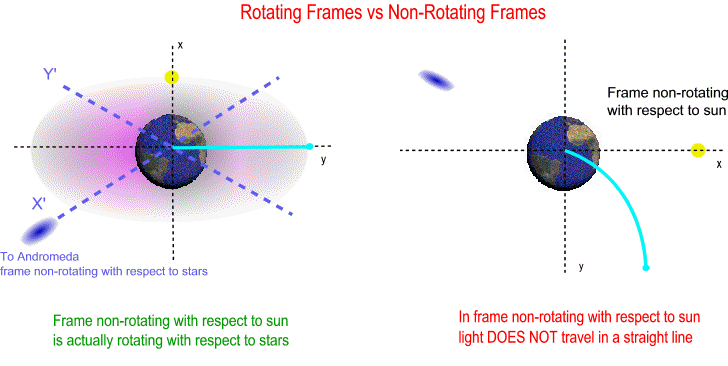
Frame non-rotating with respect to sun is actually rotating with respect to stars. From Special Relativity we know that in inertial frames light should travel in a straight line, consequently an inertial frame cannot rotate with respect to stars. Why? Because in rotating frames with respect to stars light DOES NOT travel in a straight line, and the measured speed of light in these frames is undefined (the distance traveled in one hour gives a different speed than distance traveled in two hours...). Rotating frames with respect to stars by definition are non-inertial. In General Relativity the local inertial frames where the measured speed of light is 299792.458 km/sec are actually frames non-rotating with respect to stars (not non-rotating with respect to sun). So the lunar calendar is based on the synodic system which is a rotating frame with respect to stars, and the speed of light in this non-inertial frame is undefined.
From Special Relativity we know that in inertial frames light should travel in a straight line, consequently an inertial frame cannot rotate with respect to stars. Even if a frame does not rotate with respect to stars it should not change direction (frame should travel in a straight line). However gravity's obvious effect on frames is to change their direction of travel (makes frames travel in a curve). Consider a heliocentric frame non-rotating with respect to stars, in this frame light travels in a straight line hence this is an inertial frame. But as Earth orbits the sun then this is proof enough that the geocentric frame is non-inertial.
Gravity's obvious effect on frames is to change their direction of travel however it is General Relativity that accurately describes the effects of gravity on frames of reference: Gravity causes perfectly inertial frames to rotate.

Gravity Probe B experiment confirmed that inside gravitational fields it is impossible to define a non-rotating frame with respect to stars unless this frame exits the gravitational field or it enters a gravitational freefall towards the gravitational source straight in from afar (frame-dragging + geodetic precession). This means that for any geocentric frame to be non-rotating with respect to stars Earth has either to exit the solar system or to enter a gravitational freefall towards the sun (straight in from afar).
Hence it becomes important to distinguish non-inertial motion:
1) If you are in a spaceship and fire your rockets then you are not inertial.
2) If you are orbiting the sun then a gravitational force is accelerating you towards the sun; hence you are not inertial either (even if your tangential speed around the sun remains constant).
You can find the answer in:
"There are, however, two different types of such [non-inertial] motion; it may for instance be acceleration in a straight line, or circular motion with constant speed. In the first case the magnitude of the velocity vector changes but its direction remains constant, while in the second case the magnitude is constant but the direction changes. In each of these cases the motion is non-inertial, but there is a conceptual distinction to be made."
Introduction to General Relativity', Lewis Ryder, Cambridge University Press (2009), pp 7.
So inside the gravitational field of the sun 12000 Lunar Orbits/Earth Day make 11% difference with 299792.458 km/sec when compared in a local frame non-rotating with respect to stars (sidereal system); however this frame is non-inertial. When we calculate 12000 Lunar Obits/Earth Day outside the gravitational field of the sun then this frame would travel in a straight line + would not rotate with respect to stars (becomes inertial). The difference in this local inertial frame is 0.01%.
Finally from the equivalence principle we know that there is no difference between an experiment in a local inertial frame outside sun's gravity and an experiment in a local inertial frame inside sun's gravity, that is, whenever Earth is inertial you will get the same results as if Earth is outside sun's gravity. We chose to calculate the lunar orbit outside sun's gravity because it is easier to calculate however these two experiments are absolutely identical.
You can find the equivalence principle in:
"This means that an observer in such a freely falling reference frame will say that the particles around him are not acted upon by any forces. They move with constant velocities along straight paths. In the general theory of relativity such a reference frame is said to be inertial.
Einstein's heuristic reasoning also suggested full equivalence between Galilean frames in regions far from mass distributions, where there are no gravitational fields, and inertial frames falling freely in a gravitational field. Due to this equivalence, the Galilean frames of the special theory of relativity, which presupposes a spacetime free of gravitational fields, shall hereafter be called inertial reference frames. In the relativistic literature the implied strong principle of equivalence has often been interpreted to mean the physical equivalence between freely falling frames and unaccelerated frames in regions free of gravitational fields. This equivalence has a local validity; it is concerned with measurements in the freely falling frames, restricted in duration and spatial extension so that tidal effects cannot be measured."
'Introduction to General Relativity', Lewis Ryder, Cambridge University Press (2009), pp. 15.
See the synodic system and non-inertial frames at footnote.
When the Earth-moon system is still inside the solar system the synodic frame rotates with respect to stars however when the Earth-moon system exits the solar system the synodic frame stops rotating with respect to stars. Since both the synodic and sidereal frames become non-rotating with respect to stars then the synodic periods become equal to the sidereal periods. This means that the lunar month with respect to the sun becomes equal to lunar month with respect to stars and Earth day with respect to the sun becomes equal to Earth day with respect to stars. So the 1000 lunar years with respect to sun become equal to 12000 lunar months with respect to stars.
For any valid comparison all measurements should be taken in the same frame. However most skeptics refuse to define their frame of reference, instead they use measurements taken in multiple frames. They insist on the synodic system which is a geocentric frame non-rotating with respect to sun (first frame). They use the velocity of the moon as published by NASA; however NASA uses the sidereal system which is a geocentric frame non-rotating with respect to stars (second frame). They falsely assume that the velocity of the moon in a non-rotating frame is equal to the velocity of the moon in a rotating frame. And finally they compare it to the speed of light in a local inertial frame; this is a non-rotating frame traveling in a straight line (third frame). So in the same equation they use measurements taken in THREE different frames!!! Physics wise this is garbage, all measurements should be taken in the same frame.
Length of lunar orbit = Velocity x Time (L = V T)
In a local frame non-rotating with respect to stars the velocity of the moon is not a constant. NASA measured the instantaneous velocity of the moon at various points throughout its orbit. These measurements show that the velocity of the moon varies considerably (from 3470 km/hr up to 3873 km/hr); which means that the moon accelerates and decelerates continuously. The average lunar velocity is Vavg = 3682.8 km/hr (1.023 km/sec).
The lunar orbit relative to Earth is a low eccentricity ellipse, however we cannot use the equation for the perimeter of an ellipse. Why? Because Earth lies on the major axis of this ellipse; but since the direction of the axes change with respect to stars then when the moon returns to the same position with respect to stars this does not mean that it made an exact ellipse (a local frame non-rotating with respect to the ellipse is actually rotating with respect to stars). So most astronomers calculate the length of the lunar orbit in a local frame non-rotating with respect to stars by the following equivalent circle method:
L = V T = 2 π R
⇒ V = 2 π R / T
However this velocity is under the influence of the gravitational pull of the sun. We can vectorially calculate the velocity of the moon relative to Earth without the gravitational assistance of the sun and hence the isolated length of the lunar orbit. Displacement is a vector (has magnitude and direction) and from this displacement vector we get the velocity vector (magnitude and direction); and from this velocity vector we get the kinetic energy. If external work is done we end up with a resultant displacement vector, resultant velocity vector and resultant kinetic energy. In our case we have to backtrack.
The work done by the gravitational field of the sun by creating a net rotational force on the lunar orbit (twist) is:
In a local frame non-rotating with respect to sun the moon speeds up when it heads towards the sun and then slows down by the same amount when it heads away from the sun. However in a local frame non-rotating with respect to stars the sectors where the moon speeds up and slows down are actually moving forward inside the orbit by the same angle Earth orbits the sun. In this frame there is a rotational force around Earth. This means that the moon's orbital energy is the sum of the energy acquired from this twist plus the intrinsic energy of Earth-moon system (kinetic energy of Earth's spin transferred to the lunar orbit by ocean friction).
Do you remember the oceanic high tides and low tides? Well they are caused by lunar gravity. This figure teaches you how ocean friction transfers the kinetic energy of Earth's spin to the lunar orbit:
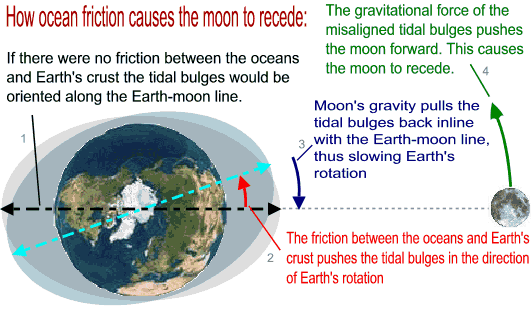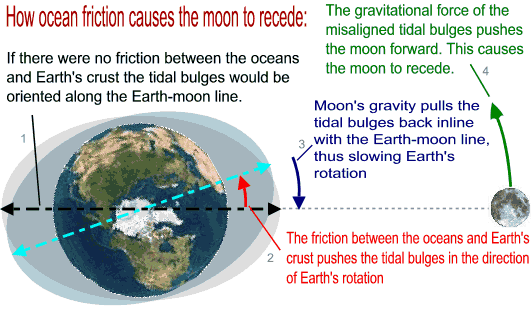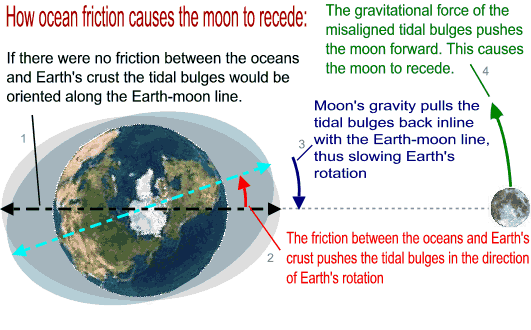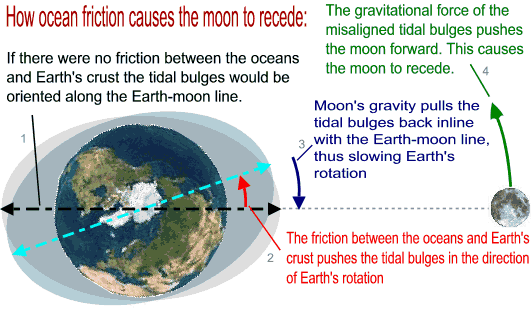
As the moon acquires more energy from Earth's spin it does not actually speed up, instead it slows down because it orbits at a higher altitude (R' increases). If Earth were spinning in the opposite direction the reverse process would have happened, the moon would have lost altitude and eventually crashed into Earth.
Today's lunar orbit is a very low eccentricity ellipse (very close to a perfect circle) but when the moon first formed it was a very high eccentricity ellipse. The eccentric ellipse back then had a point very close to Earth and another point very far out. When the moon was nearest to Earth inside the ellipse the gravitational forces were stronger and hence more energy was transferred to the moon when it was closer to Earth than when the moon was farther out inside the ellipse. This made the moon recede more when it was closer to Earth than when it was farther out inside the ellipse. This difference in recession rates smoothed out the differences between the closest and the farthest points in the orbit (this is why today's lunar orbit is very close to a perfect circle). So for each direction the recession has different magnitude. Since this recession has magnitude and direction then it is a displacement vector (R'). However in every direction this displacement vector is normal to the rotational force around Earth (always at right angles with the rotational force around Earth, 90 degrees). Since the resultant R is the sum of two normal displacement vectors then those displacement vectors form a right triangle. We can use trigonometry to solve those displacement vectors:

By definition in a right triangle cosθ = side adjacent / hypotenuse.
⇒ side adjacent = hypotenuse cosθ
⇒ R' = R cosθ
We can verify this triangle by the Pythagorean Theorem:
(R sinθ)2 + (R cosθ)2 = R2sin2θ + R2cos2θ = R2 (sin2θ + cos2θ) = R2 (1)
Hence cosθ is the only solution to this restricted three-body problem.
To learn why there are two tidal bulges, one facing the moon and another one opposite to it, see spherical mass at footnote.
The lunar orbital radius R is a function of total energy, however the total orbital energy comes form two sources: ocean friction and gravitational twist (two sources, not one). As the distance to the sun increases to infinity the lunar orbit loses this twist; but without the energy gained from this twist the orbital radius decreases to R' = Rcosθ.
You might ask why can't the moon simply remain at radius R and velocity Vcosθ? Well the answer to this is actually counter intuitive. If you were driving a car and apply brakes then the car will decelerate (lose kinetic energy). But if you apply brakes to the moon (lose kinetic energy) the moon will slow down for a while however it will become unstable (shortage in kinetic energy). The moon that was at the right velocity around Earth now becomes a little bit too slow for Earth's gravitational force (too high too slow). To compensate for this imbalance the moon descends to a lower altitude (trades excess potential energy above Earth with kinetic energy). After descending a bit the moon speeds up and returns to equilibrium. So contrary to driving a car, if you apply brakes to the moon it will eventually speed up! This might sound crazy however it is true. In our case the orbital radius decreases to R' = Rcosθ and the moon accelerates to V' = V/(cosθ)1/2.
The ratio of the orbital binding energy (the ratio of the work required to move the moon against gravity to infinity) is:

This means that without the energy gained from this twist the orbital radius decreases to R' = Rcosθ. Hence when inertial the length of the lunar orbit becomes L' = 2πR' = 2πRcosθ = Lcosθ and the orbital period decreases (see gravitational assist at footnote).
Today when the moon makes 360 degrees around Earth with respect to stars the Earth-moon system moves 26.92952225 degrees around the sun. Hence the lunar orbit's twist angle θ = 26.92952225 degrees. We can calculate θ from the period of one heliocentric revolution of the Earth-moon system (365.2421987 days):
θ = (360 degrees / 365.2421987 synodic days) x 27.32166088 synodic days = 26.92952225 degrees
Similarly, Earth's spin slows down by 6 seconds i.e. when inertial Earth day t' becomes 86170.43114 sec (see Earth's spin at footnote).
So finally we can check the accuracy of this equation:
C t' = 12000 L'
The distance traveled by light in one Earth Day = C t' = 299792.458 km/sec x 86170.43114 sec = 25833245358 km
The distance of 12000 lunar orbits = 12000 L' = 12000 x 3682.8 km/hr x 655.71986 hr x cos(26.92952225) = 25836303825 km
By dividing the two distances we get the ratio of 1.00011839267.
12000 Lunar Orbits/Earth Day = SPEED OF LIGHT
What would happen if Earth suddenly stopped in its track while orbiting the sun? Earth would plummet into the sun, right? If it were not for distant stars then how would you know that Earth is orbiting the sun? Maybe it is the sun that is orbiting Earth. Or better yet, maybe Earth and sun are both fixed in their positions. So how do you know? It is the background of distant stars that tells you which is orbiting which.
Our physics today simply does not work with the synodic system. For example, this equation gives you the distance to the moon by simply knowing the sidereal lunar month (27.3 days):

If you use the time for synodic lunar month (29.5 days) it gives you the wrong distance to the moon (consequently wrong energy, wrong momentum...). But what you should keep in mind is that the equations in the sidereal system have no counterpart in the synodic system.
Although the moon keeps facing Earth it is actually spinning with respect to distant stars. Since the moon is spinning then it should bulge at the equator, right? However an observer on Earth sees the bulge but does not see the spin of the moon. When we calculate the bulge from spin with respect to Earth we get the wrong value (does not match observation). When we calculate the bulge from spin with respect to the sun we also get the wrong value. However when we calculate the bulge from spin with respect to distant stars we get the correct value. This should tell you that the bulge is a consequence of the spin with respect to distant stars (neither with respect to Earth nor with respect to the sun). This is why classical orbital mechanics (and general relativity) are based on the sidereal system, that is, rotation (and precession) are with respect to stars.
Some skeptics argue that due to Earth's motion around the sun the length of the lunar orbit is longer for an observer on the sun, however this is also false. Why? Because the distance between Earth and the moon (R) is the same whether measured from Earth, from the sun or from the center of another galaxy... And since the length of the lunar orbit is simply 2πR then the length of the lunar orbit is the same for an observer on the sun, on the moon, Andromeda... Actually you should deduce from the above equation that R is measured the same for any observer in the Newtonian limit (non-relativistic).
The sidereal system is a local frame non-rotating with respect to stars. The difference between a local frame non-rotating with respect to stars and a local frame non-rotating with respect to the CMB is extremely negligible and cannot change the result. The effect of our galaxy is also too small to make any difference. The only thing that really matters is the effect of sun's gravity on our local frame of reference.
Consider a spherical mass of weakly-interacting particles (say a gas) and a spherical gravitational source (say the moon). The gravitational force is stronger on the particles of gas closer to the moon than on the particles of gas farther out. The difference in forces makes the sphere of gas to be stretched into an ellipsoid. (General relativity explains why the actual tidal effect generated by a spherical gravitational source is stretching in the radial direction and additional squeezing in the transverse direction). In our case the moon stretches the oceans into an ellipsoid while Earth is too rigid to change shape; so we end up with two tidal bulges one facing the moon and another one opposite to it. This is why we have two high tides a day instead of one.
You might ask why does the much stronger gravitational force of the sun actually produce much smaller tidal bulges than the moon? Well it is not the magnitude of the forces that causes the stretching but rather the difference in forces. Although the sun's gravitational forces are stronger in magnitude, the much bigger distance to the sun causes this difference in forces to be much smaller; hence the weaker stretching and smaller bulges. If the radius of the oceans (or the sphere of gas) was as big as the radius of the lunar orbit then the sun's average gravitational force on the particles closer to and farther out from the sun would be the same as it is today but the increased difference in forces would stretch this sphere into an ellipsoid with bulges thousands of kilometers high. This ellipsoid will always be oriented towards the sun; but as Earth goes around the sun the position of the sun relative to Earth with respect to stars changes. This means that with respect to stars this ellipsoid will always be rotating in order to point to the sun again; this rotation with respect to stars is rotational kinetic energy. As the distance to the sun increases to infinity the position of the sun relative to Earth with respect to stars remains the same, hence as the distance to the sun increases this sphere of particles will lose this twist. This means that sun's gravitational field along with Earth's motion around the sun produce a net rotational force on this sphere of particles (gravitational twist). So the sun exerts gravitational twist on the Earth-moon system in the same way that Earth exerts gravitational twist on the moon.
Sun's gravitational field along with Earth's motion around the sun produce a net rotational force on the lunar orbit (like torque around Earth). Without this gravitational assist the moon's isolated orbital length would only be L' = Lcosθ:
This restricted three-body problem is similar to the 1973 Pioneer 10 spacecraft gravitational assist by Jupiter. The data published by NASA show that the kinetic energy of the spacecraft increased five folds (enough to exit the entire solar system). This increase in kinetic energy came from Jupiter's motion around the sun.
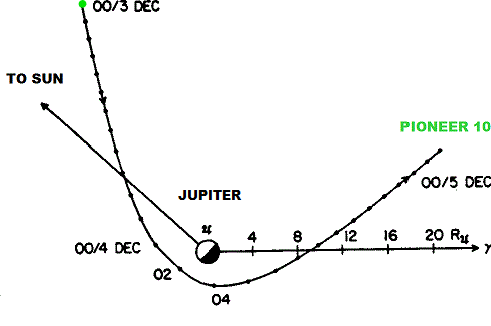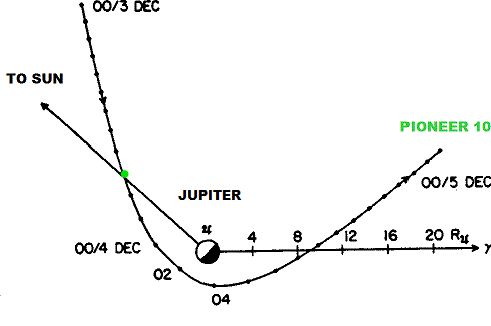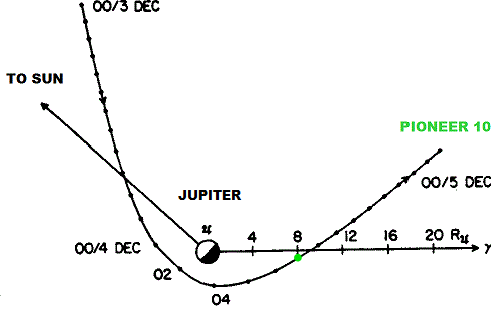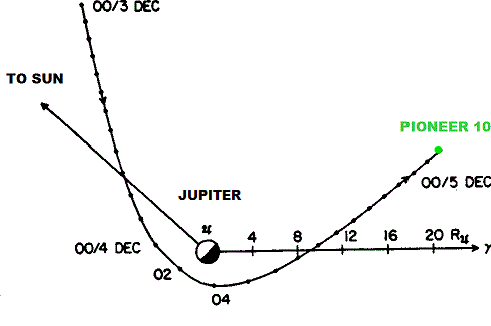
In a Jupiter centered frame non-rotating with respect to sun the speed of the satellite before the encounter was equal to the speed after the encounter (change in direction only); however this frame is rotating with respect to stars. In a heliocentric frame non-rotating with respect to stars (inertial frame) the kinetic energy of the satellite increased five folds, enough to escape sun's gravity.
The approach to Jupiter was in the same direction as the moon orbits Earth around the sun. The only difference between the two gravitational assists is that Pioneer 10 had an open orbit while our moon has a closed one. In this closed orbit the increase in kinetic energy makes our moon orbit at a higher altitude above Earth. So when the Earth-moon system is inertial (without this assist) the moon should orbit at lower altitude.
Also the data published by NASA show that the velocities before and after the gravitational assists can be calculated vectorially, that is, you can use trigonometry to calculate the magnitude and direction, and hence the kinetic energy.
In a geocentric frame non-rotating with respect to sun the moon speeds up when it heads towards the sun and then slows down by the same amount when it heads away from the sun. However in a geocentric frame non-rotating with respect to stars the sectors where the moon speeds up and slows down are actually moving forward inside the orbit by the same angle Earth orbits the sun. In this frame there is a rotational force around Earth; a twist or gravitational assist.
This rotational force is evident in the NASA animation of Swift J1644+57, a star consumed by a black hole:
In this example the direction is different but the dynamics are the same. The gravitational force is stronger on the particles of gas closer to the black hole than on the particles of gas farther out. The difference in forces stretches the sphere of gas into an ellipsoid. But this ellipsoid will always be oriented towards the black hole. So as this star goes around the black hole the position of the black hole relative to the star changes. This means that in a star centered frame non-rotating with respect to distant stars this ellipsoid will rotate in order to point to the black hole again. This rotation with respect to distant stars is rotational kinetic energy. The star's Hydrogen gas gains energy and orbits higher above the star. A point is reached where gravity of the black hole becomes dominant and steals this gas away from the star.
Earth is spinning with respect to stars much faster than the moon is orbiting Earth. This makes the angle between Earth's inertial and accelerated vectors to be different than that of the moon. Today when Earth rotates 360 degrees on its axis with respect to stars Earth moves 0.9829560917 degrees around the sun. Hence Earth's twist angle α = 0.9829560917 degrees.
α = (360 degrees / 365.2421987 synodic days) x (86164.0906 sec/86400 sec) synodic days = 0.9829560917 degrees
Just like when the moon recedes from Earth its spin slows down also when Earth recedes from the sun its spin slows down, that is, its rotational kinetic energy decrease. So as the distance to the sun increases to infinity Earth day increases to t' = t/cosα.
The ratio of the work required to stop Earth's rotation is:

This means that without the energy gained from this twist Earth day increases to t' = t/cosα = 86170.43114 seconds (6 seconds increase from 86164.0906 sec).
Drag & Drop Website Builder